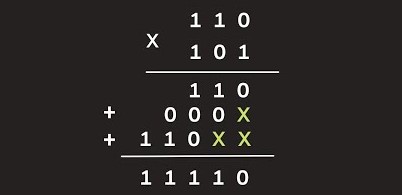Simplify your numeric tasks using our Binary Translate Math Calculator. Easily convert binary digits to decimal numbers and vice versa, ensuring accuracy and efficiency.
RESULTS
Struggling with binary numbers can be a real problem for students and professionals alike. Enter the binary translate math calculator, an innovative tool that simplifies this complex process.
Our guide will help you on the path from confusing strings of zeroes and ones to clear, understandable decimal values.
Understanding Binary Numbers
It’s this simplicity yet profound versatility that enables us to perform complex calculations and operations within digital environments, a knowledge essential for anyone involved in computer programming or mathematical computations.
What is a binary number?
A binary number is made up of only two digits, 0 and 1. These numbers are the core of the binary system, which is also known as base-2. Each digit in a binary sequence increases in value based on its position from right to left.
The values double each time, moving from 2^0 (which equals 1) to higher powers like 2^1 (equals 2), then to 4, 8, and so on.
Computers use these numbers because they can read them as off (0) or on (1). This system fits well with digital electronics that work with two states: high voltage for a ‘1’ and low voltage for a ‘0’.
Binary makes computer programming and design simpler. It turns complex instructions into strings of zeros and ones that machines can understand quickly.
Converting to and from binary numbers
To change a binary number to a decimal, you multiply each bit by two. The power depends on the bit’s position. Then you add up all those results. It’s like turning “on” and “off” switches into numbers we use every day! Changing back from decimal to binary is another process.
You divide your number by two again and again until you can’t anymore. Each time, write down the remainder, it’s either zero or one.
Next, let’s dive deeper into how these conversions work with specific examples for clarity!
Benefits of Using a Binary Calculator
A binary calculator streamlines the process of translating complex binary math into actionable results with unparalleled precision—discover how it can revolutionize your computational tasks.
Saves time and effort
You’ll get quick results with a binary calculator. It changes numbers from decimal to binary and back fast. This tool lets you skip the tough math and focus on solving problems instead.
You won’t make mistakes that can happen when you work out the numbers by hand.
Imagine turning long calculations into a few clicks! With this calculator, accurate answers are just seconds away, making it perfect for homework or projects. Look forward to tackling arithmetic operations like binary addition or subtracting without stress.
Now ready yourself for learning about accurate calculations next!
Accurate calculations
Binary calculators are built to handle the precision needed for binary number operations. They can crunch big numbers and complex problems without making mistakes. This means you get reliable results every time you use them.
Math in the binary system, like addition, subtraction, multiplication, and division, is a breeze with these tools.
These calculators take care of all the hard work when converting between decimal and binary systems. You no longer have to struggle with long manual calculations or worry about human errors.
Trust a binary calculator to give you speedy and exact answers for your math challenges. Refine your mathematical precision with our Factorial Calculator. Seamlessly compute factorials for accurate results.
Easy conversions
Converting numbers between binary and decimal systems becomes a breeze with a binary calculator. Forget the stress of long division or multiplication by hand. Just type in the number, click calculate, and get your answer fast.
Your math homework or coding project gets easier because you have a tool that does the tricky part for you.
Switch from base 2 to base 10 and back without having to learn complex rules or steps. The calculator handles all forms of binary arithmetic quickly and accurately. It’s like having a math expert who specializes in binaries right at your fingertips! Whether for schoolwork or tech tasks, this user friendly device saves precious time so you can focus on other important work. Enhance your numerical efficiency with our Octal to Binary Calculator. Streamline conversions effortlessly for accurate results.
Common Arithmetic Operations with Binary Numbers
Mastering these binary techniques—addition, subtraction, multiplication, and division is essential for anyone looking to thrive in fields ranging from computer science to electrical engineering.
Addition
To add binary numbers, you follow rules like those for adding decimal numbers. You put one number above the other, lining up the place values. Then you start from the right and move left, adding each pair of digits together.
If a sum is 2 or more, it carries over to the next higher place value.
Let’s say we’re adding 1011 and 1101 in binary. We write them on top of each other and add each column:.
1011
+ 1101
——
Starting on the right, we have 1 plus 1 equals “10” in binary, so we write down 0 and carry the 1. Move to the next column where our carry over makes three ‘ones’. This also becomes a “10” with another carryover:.
*11 (carried over)
1011
+ 1101
——
*00 (sum)
Keep going until all columns are added up:
**111 (carried over)
1011
+ 1101
——
10000 (final sum)
Our final answer is “10000” in binary! Using a math calculator that handles basic arithmetic operations can make this process much faster and reduce mistakes. It turns tricky binary addition into simple clicks—just enter your numbers and get instant results!
Subtraction
Subtracting binary numbers is like taking away blocks from a pile. You work from right to left, just as you do with the numbers we use every day. If you need to take one block from an empty space, borrow ten blocks from your neighbor on the left and keep subtracting.
Remember, in binary math, ‘ten’ means two. This process of borrowing works just like in decimal subtraction but uses powers of 2 instead.
You might see a bunch of 1s and 0s and think it’s tricky to figure out how much is left after taking some away. But once you get the hang of it, binary subtraction becomes easy peasy! It all comes down to knowing when to borrow that extra set of blocks (or in this case, bits).
Keep practicing with different numbers and soon enough, you’ll be quick as lightning at subtracting those pesky binaries!
Multiplication
Multiplying binary numbers is similar to multiplication in the decimal system but simpler. You only need to know how to multiply by 0 or 1. Start by multiplying each bit from one number with every bit of the other, just like long multiplication in decimals.
Line up the results and add them together.
You’ll sometimes carry over a digit when your answer goes over ‘1’, because binary digits can only be 0 or 1. Each step holds power as you move left, doubling every time: from ones, to twos, fours, eights, and so on.
This method lays out a clear path for calculations involving binary multiplication without confusion or error.
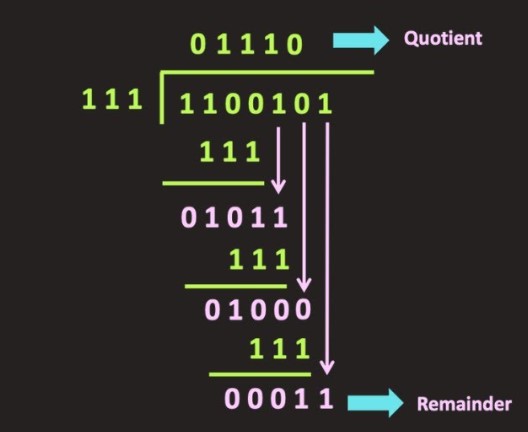
Division
Division is a crucial step in binary arithmetic, just like adding, subtracting, and multiplying. It splits one binary number by another. You get two results: a quotient and sometimes a remainder.
Think of it as sharing cookies among friends; if you have some leftover, that’s your reminder.
Using the Binary Translate Math Calculator makes this process much easier. You don’t have to struggle with the complex steps of binary division independently; this calculator does the hard work for you.
It divides quickly and gives correct answers every time. Whether you’re learning about computer systems or working with digital electronics, knowing how to divide binary numbers is key.
This tool will help get accurate results fast without any mix ups! Unlock binary transformations with our Text to Binary Calculator. Seamlessly convert text into binary code for accurate results.
Step by step Guide On How to Use The Calculator
Using a binary translate math calculator is simple and straightforward. Here’s how you can quickly convert binary numbers:
- First, find the input field on the calculator.
- Now, type your binary number into this field.
- Next, look for the options to choose between ASCII or UTF 8 Unicode.
- Pick the one that suits your needs.
- After selecting, click on the “calculate” button.
- Wait a moment for the calculator to work.
- Soon, you’ll see your translated text appear as a result.
Examples
Now, let’s put the calculator to work. Imagine you have two binary numbers: 1010 and 0110. You want to know their sum and difference in both decimal and binary forms. First, you would type 1010 into the calculator.
Then, add 0110 in the next field for addition or subtraction. Hit calculate, and like magic, you see your answers! For the addition of 1010 and 0110, it shows a decimal number of ’16’ and a new binary number ‘10000’.
For subtraction, it gives you ‘4’ in decimal form and ‘100’ as the binary result.
The Binary Translate Math Calculator is great for quick checks or homework help. It turns tricky binary problems into easy math that anyone can understand. With this tool, converting between numeral systems is no longer daunting, it becomes simple and fast! Optimize hexadecimal conversions with our Hex to Binary Calculator. Seamlessly convert hex values to binary code for accurate results.
FAQs
1. How can I convert a binary number to a decimal?
To change a binary numeral to a decimal, your calculator multiplies each digit by its power of 2 based on its position, starting from right to left and then adds them all up for you! This gives you the numerical value in our familiar base-10 system.
2. Can I turn my regular numbers into binary with this calculator?
Absolutely, you can take any real number (even those with decimals) and find out what it looks like as a string of 1s and 0s! Just input your figure into the conversion feature, which breaks down your value using weighted averages and scientific notation, then displays your fresh new sequence of binary digits.
3. Is there more than just converting? Can this tool help me understand other aspects of binaries?
For sure, it decodes more complex concepts too! Decimal places switch seamlessly between systems; additionally, concepts such as antilog, arcsin, arccosine, tangent, and their inverses like arctan are within reach thanks to insightful explanations paired with clear cut calculations!
Related Calculators: